|
|
#107年,#37期,#數學,# 甲組,#警專, |
| |
設α,b皆為正實數,則(α+2b)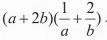 之最小值為? 之最小值為? |
|
|
#107年,#37期,#數學,# 甲組,#警專, |
| |
已知空間中三點A(l,一1,2),B(2,3,l),C(4,3,2),則ΔABC的面積最接近下列何者? |
|
|
#107年,#37期,#數學,# 甲組,#警專, |
| |
已知點A(l,2,3),B(3,2,l),平面E:x-2y+2z=k。若A,B位在平面E之異側,且「A到平面E的距離」大於「B至平面E的距離」,則k可為下列何值? |
|
|
#107年,#37期,#數學,# 甲組,#警專, |
| |
假設空間中兩相異平面E1,E2皆通過(5,2,0)與(4,3,8)兩點,試問以下哪一個點不會同時在E1與E2上? |
|
|
#107年,#37期,#數學,# 甲組,#警專, |
| |
設.jpg) ,若B2的反矩陣不存在,則實數x=? ,若B2的反矩陣不存在,則實數x=? |
|
|
#107年,#37期,#數學,# 甲組,#警專, |
| |
在一伯努利試驗中,每次試驗成功的機率為p。若重複此試驗n次,且每次試驗的結果皆是獨立的,則下列哪一敘述是錯誤的? |
|
|
#107年,#37期,#數學,# 甲組,#警專, |
| |
設f(θ)=2cosθ-√5sⅈnθ+1的最大值為x、最小值為y,則x-2y之值為? |
|
|
#107年,#37期,#數學,# 甲組,#警專, |
| |
計算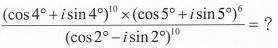 |
|
|
#107年,#37期,#數學,# 甲組,#警專, |
| |
計算.jpg) |
|
|
#107年,#37期,#數學,# 甲組,#警專, |
| |
若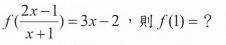 |
|